In recent years, the world has faced several public health issues, including the uneven distribution of medical resources, life-threatening chronic illnesses, and rising operational costs. Heart failure is considered a more severe and lethal disease than others. It has been assumed that it is a chronic condition worldwide. Integrating current technology into the healthcare system will substantially aid in resolving the challenges. Data mining is a method of identifying fascinating patterns in current data in various scenarios to turn the data into valuable information. Take the patient’s data set and get the results to see if the doctors need to diagnose the patient. This work employs a hybrid deep learning model to provide large data analysis and visualization techniques for heart disease detection. Using Apache Hadoop as the development platform, the suggested framework for heart disease prediction is displayed in Fig. 1. An enhanced k-means clustering (IKC) method removes outliers before analyzing the curated medical data. Recursive feature elimination (RFE) is then used to identify the most important features once the distribution classes have been balanced using the synthetic minority over-sampling method (SMOTE). Ultimately, the bio-inspired hybrid mutation-based swarm intelligence (HMSI) model employs an attention-based gated recurrent unit network (AttGRU)to forecast diseases.

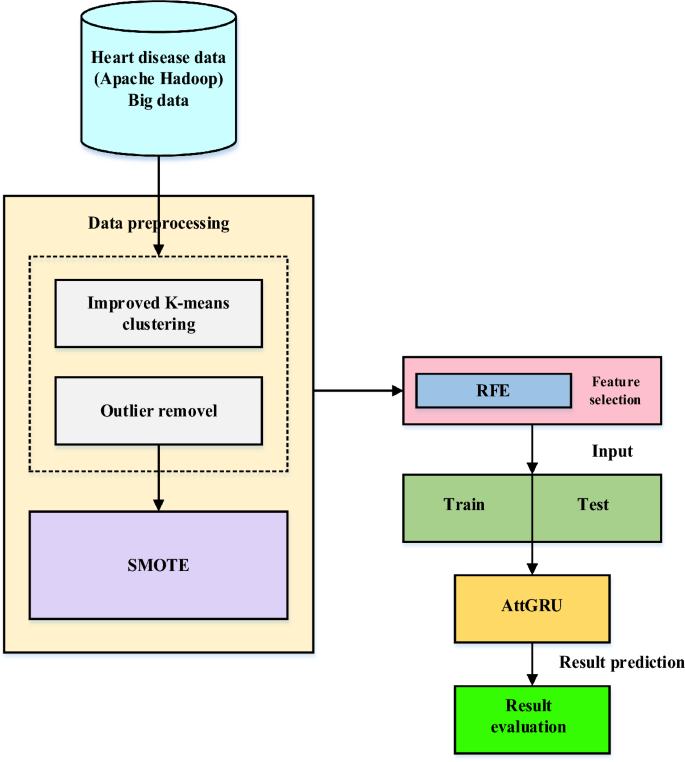
Proposed heart disease prediction framework.

Apache hadoop

This paper describes the most often used formats for storing large datasets in the Apache Hadoop system and provides approaches for determining the best storage formatfor this framework by combining experimental assessments and topical optimizations. This article takes a close look at the common file formats used in the Apache Hadoop system to store big datasets. Choosing the best possible storage format is critical as the amount of data handled in distributed computing settings grows. The most widely used storage formats are surveyed in this study, but it goes one step further and suggests methods for determining which format works best inside the Hadoop framework. In order to find astorage format that is in perfect alignment with the unique needs and subtleties of Apache Hadoop, the methodology used in this research combines targeted optimizations with empirical assessments. Through the exploration of experimental assessments and subtle improvements, this work adds to the current discussion on storage strategy optimization in large-scale distributed computing environments, offering insightful information to researchers and practitioners navigating Apache Hadoop’s complicated big data storage landscape.

MapReduce algorithm

A reduced algorithm leverages parallel programming to process a large dataset map. Distributed and parallel processes can reduce network performance, fault tolerance, and load balancing. Apache Hadoop, an open-source project, implements MapReduce in Java to provide greater consistency and scalability. The use of a sizable dataset is necessary to take the field a step further and apply advanced processing methods to the context of cardiac health. A simplified solution that uses parallel programming is essential to handle the large amount of data in datasets relating to hearts. Through the use of parallel processing, the method may take advantage of the simultaneous execution of tasks, resulting in a considerable speedup in the computing of intricate analyses and forecasts.

The efficiency and dependability of data processing are directly impacted by network performance, fault tolerance, and load balancing in the field of heart disease analytics. For the purpose of reducing difficulties brought on by these elements, distributed and parallel operations are essential. Optimal system performance is achieved by strategically allocating computing jobs among several nodes, which also strengthens the system’s resistance against error. Load balancing guarantees an equal distribution of computing demands to eliminate bottlenecks and maximize resource utilization. The MapReduce paradigm was introduced by Apache Hadoop, an open-source framework that is well-known for its ability to handle giant datasets. An effective method for distributed processing is provided by this programming model, which is implemented in Java inside the Hadoop environment. Large-scale dataset processing may be made more consistent and scalable with MapReduce by decomposing complicated calculations into jobs that can be mappable and reducible. The utilization of Apache Hadoop and MapReduce in the context of heart disease research expands the possibilities for novel insights and solutions in the field of cardiac health analysis by providing a stable infrastructure that can easily navigate the complexities of parallel computation.

The MapReduce algorithm includes the following steps:

1. 1.

   Data collection: a large dataset is given as input.

2. 2.

   Splitting: for each dataset, key-value pairs are generated.

3. 3.

   Mapping: for each dataset, another set of key-value pairs is generated.

4. 4.

   Sorting: The key-value pairs are grouped depending on how they are associated.\

5. 5.

   Reduce: the number of key-value pairs is reduced to a single key-value pair for a unique group.

6. 6.

   Outcome: the result is minimized and stored in the database.

Improved k-means clustering algorithm

A cluster of related data can be determined by finding the components’ mean values within each cluster subset, which is then assigned as the cluster center coordinate. This process is applied for the outlier elimination procedure, as shown in Fig. 2. The evaluation cluster categorical criterion function iteratively splits the element set into multiple clusters. When the function attains its peak value, the iteration completes²⁴. The k-means procedure flow chart is detailed as the following.

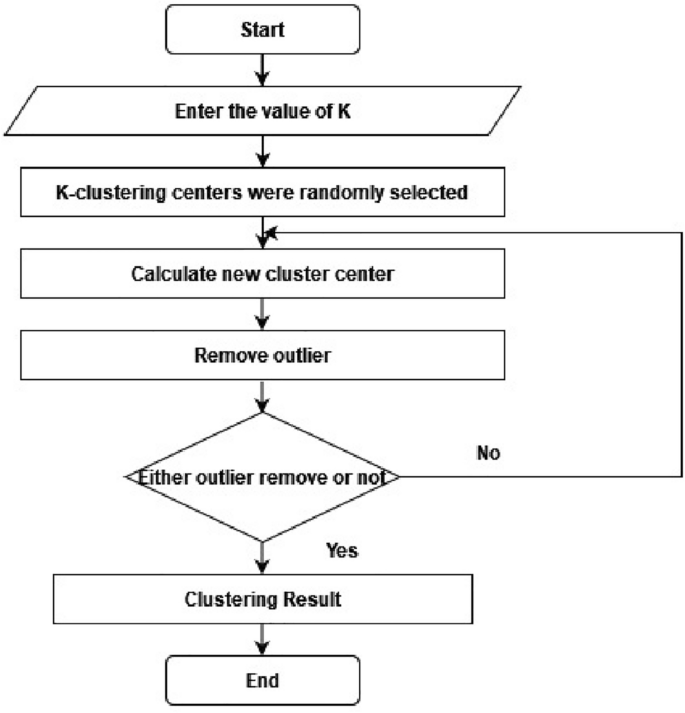
A flowchart for outlier removal using k-means clustering.

Step 1: Randomly select K items from the data components to initiate cluster centers:

Step 2: Calculate the distance between all components in a cluster and \({S}_{r}(I)\):

If the following minimization requirement is met, then assign it to the nearest cluster:

then, \(x_{q} \, \in \,C_{k}\).

Step 3: Calculate the error square sum criterion:

Step 4: If \(|J_{c} (I) – J_{c} (I – 1)| < \xi\), then stop and output the clustering result. Otherwise, continue iterating by again calculating the clustering center \(S_{r} (I) = \frac{1}{n}\sum \sum\nolimits_{j = 1}^{{n_{r} }} {x^{r}_{k} }\)\(,\) and returning to step 2 until you reach step 2.

This IKC process describes and evaluates the identified clusters to guide the removal of outliers from medical data. This technique can be enhanced by adjusting the initiation strategy when overlaps in the clusters exist in the data. In this scenario, the K-means algorithm can further enhance the results of the starting procedure²⁵.

Outlier removal in K-means clustering

The process for removing outlines from the K-means cluster is straightforward. After the K clusters are identified, calculate the accuracy and silhouette index. Next, the smallest cluster is identified and regarded as outlier data. These outlier clusters are expected to be few in their count or notably different from the other clusters. These outliers clusters are eliminated from the dataset, and the k-means cluster accuracy and silhouette index are recalculated²⁶.

Synthetic minority over-sampling technique (SMOTE)

The SMOTE approach is applied during data preprocessing to remove missing values before normalization with the conventional scalar approach to managing imbalanced data present in the source input.SMOTE is frequently used for developing a classifier with an imbalanced dataset, often seen with an unevenly distributed underlay of output classes. Multiple versions of the technique have been developed to improve its dependability and adaptability for various use cases. SMOTE executes interpolation within a dataset’s minority classes to increase their quantity, which adds to the generalization of classification²⁷.

Feature selection

In machine learning, a popular feature selection method called Recursive Feature Elimination (RFE) is used to improve model performance by methodically removing less significant features. In RFE, the model is fitted several times, with the least important feature eliminated each time, and the effect on the model’s performance is evaluated. This iterative procedure is carried out until the target feature count is attained. RFE aims to increase model interpretability, decrease overfitting, and boost computing efficiency by concentrating on the most important attributes for producing precise predictions. It helps to choose a subset of features that contribute most to the model’s predictive power, which eventually results in more effective and efficient machine learning models. It is beneficial in situations involving high-dimensional datasets.

We employed the RFE approach to obtain the essential aspects of a prediction, which is frequently used because of its ease of implementation and efficiency in identifying significant features in training datasets and discarding ineffective features. The percent RFE approach identifies the most important characteristics by identifying high correction among certain variables and the objectives (labels). After calculating missing values, determining the relevant aspects with significant and positive links to illness diagnosis features is necessary. Extracting vector features eliminates unnecessary and irrelevant features from the prediction, which would otherwise preventaviable investigative model.

Recursive Feature Elimination (RFE) may be used to improve the predictive modelling process in the context of a heart disease dataset by pinpointing the most crucial characteristics for precisely forecasting the existence or absence of heart disease. Here’s how RFE may be applied to the examination of a dataset on heart disease:

Investigation of datasets

Explore the heart disease dataset first, becoming familiar with the characteristics that are accessible, their categories and numerical representations, and the goal variable (which indicates if heart disease is present or absent).

Preprocessing of data

Carry out the required preprocessing actions for the data, such as addressing missing values, encoding category variables, and scaling numerical characteristics as required.

Using RFE

Utilize a machine learning model (such as decision trees, logistic regression, or support vector machines) in conjunction with Recursive Feature Elimination (RFE) to Recursive Feature Elimination (RFE) is used in conjunction with a machine learning model (e.g., logistic regression, decision trees, or support vector machines) to rank and choose features based on the degree to which they improve the model’s performance. Using the RFE approach, the model is iteratively fitted, each feature’s relevance is assessed, and the least important feature is eliminated.

Attention-based gated recurrent unit network (AttGRU)

The attention mechanism in machine learning techniques arose from the idea that while identifying something in its environment, a human gives greater attention to only particular portions of the surroundings. This model structure is widely used in natural language processing across a wide range of applications. However, a few studies have employed the attention mechanism in conjunction with the gated recurrent unit (GRU) network to predict economic series regularly influenced by several complicated factors simultaneously. In this use case, not all components in the input series are equally essential to the expected value during each time step when projecting energy prices. Therefore, instead of treating all elements equally, the attention mechanism focuses on meaningful information to execute prediction processes. Figure 3 outlines the three phases for computing an attention value, which can be used to learn how to deliver varied weights of the input series items at different periods. For instance, the strategy has been stated in the following manner²⁸.

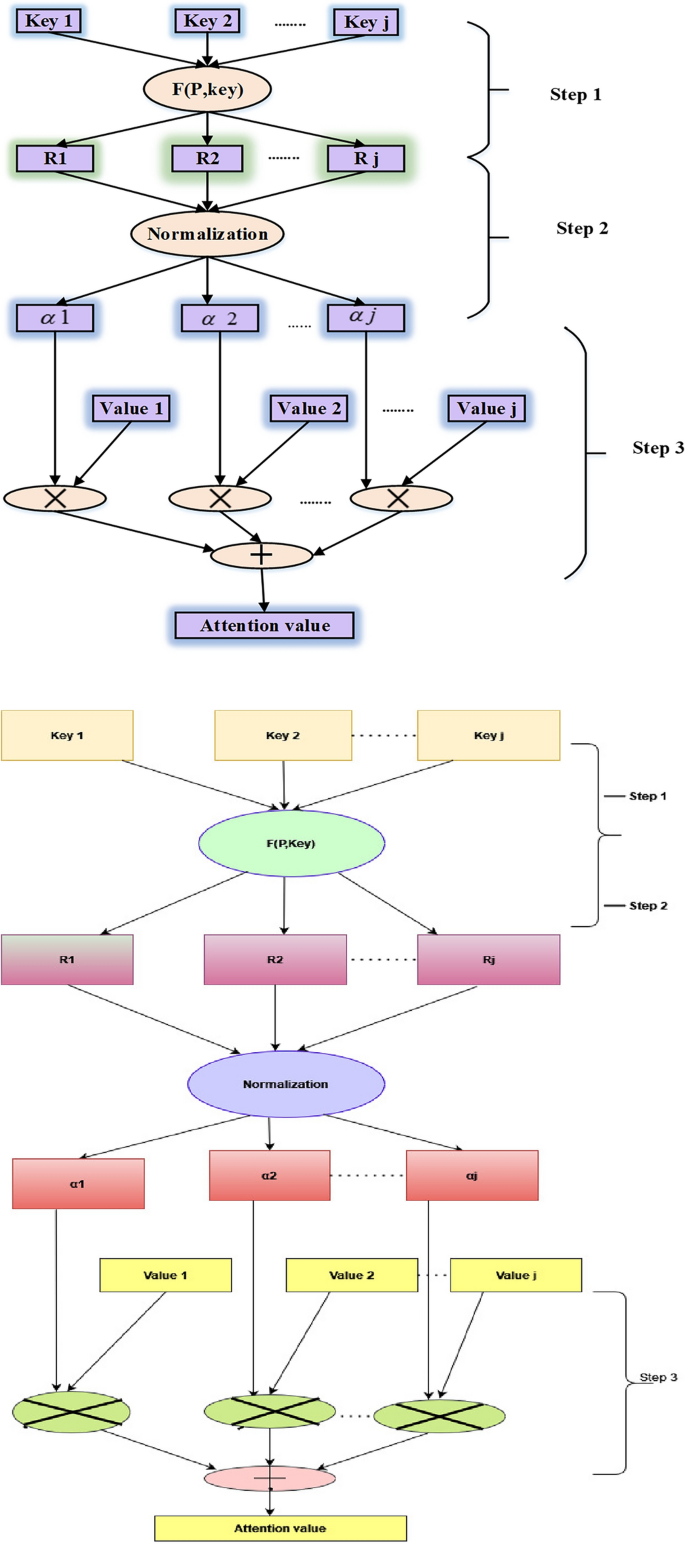
Three steps for calculating the value of attention.

Step 1: Determine the relevance of \(J_{tr} ,r = 1,2,…,r\) for each earlier input element and output element at time \(t\), indicated by the attention score \(e_{tr} = Attend(x_{tr} )\).

Step 2: The softmax function is utilized to transform the relevance into a probability, and the attention weight of every element in the input sequence at any given moment is represented by \({\alpha }_{tr},\)

Step 3: To account for the influence of the constituents on the expected value, multiply the likelihoods acquired in Step 2 by the intrinsic interpretation of the pertinent input components. Next, add all of the input contributions to the next value’s prediction as the input components. As the neural network’s input, the weighted feature is used and represented as

Gated recurrent unit (GRU) network

Without sacrificing its benevolence, the GRU network recreates the gating mechanism of the LSTM cell. Each and every GRU cell has an update gate (b_t) and a reset gate (j_t). Timing patterns in the data may be recorded because the reset gate, like the LSTM, regulates how much previous information is retained instantly and how much new information is introduced. An arbitrary quantity of data may be quickly memorized via the update gate, which also regulates how much past information is “forgotten.” Fig. 4 illustrates the fewer limitations in a GRU cell than in an LSTM cell, suggesting that the GRU creation process is less complicated than the LSTM formation process. It is possible to use the GRU network to tackle the problem because it is derived from the LSTM network.

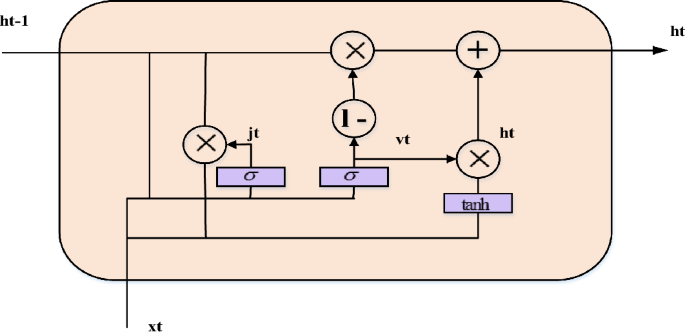
The structure of a GRU network.

The fundamental steps for a GRU network are outlined in the following. First, the most recent input \({x}_{t}\) and the obscure state created by the preceding cell \(h_{t – 1}\) establishes the reset gate \(j_{t}\) and update gate \(v_{t}\) at the existing state at time \(t\). The two gates’ outputs are;

In this case, the appropriate weight measurement matrices are and, the bias vectors are and, and the sigmoid function is σ.

Second, one way to characterize the candidate’s disguised condition at this time is as

where \({\text{tanh}}\) is the hyperbolic tangent function, \({w}^{h}\) are the relevant weight coefficient matrices of the hidden layer, \({b}^{h}\) is the associated bias vector, and * denotes the matrix dot multiplication between the matrices.

Finally, the existing hidden state \({h}_{t}\) output is assessed by a linear combination of the current candidate’s hidden state \({\overline{h}}_{t}\) and the preceding hidden state \({h}_{t-1}\), with the total weighted measurements equal to unity,

Methods of machine learning are dynamic since they usually involve several parameters that need to be adjusted to achieve the best results. By choosing the optimal weight values, this article enhances the performance of the AttGRU model, which would otherwise need time-consuming manual optimization of the data and model parameters. Here, the GRU network topology is proposed as follows: an input layer, a fully connected layer, two layers of an AttGRU hidden layer, and an output layer. Additionally, the AttGRU network’s weights and biases are optimized during the model training phase via the HMSI technique, which is covered in the following section. The GRU model hyperparameters are the time step, batch size, and number of hidden layer units in this model. The mean absolute percent error of the model determines the prediction fitness value.

where \(n\) isthe population size,\(E_{i}\) denotes the sample output value, and \(e_{i}\) represents the actual output value.

Bio-inspired hybrid mutation-based white shark optimizer (HMWSO)

The location of the food supply in each search area cannot be determined, though. In such a situation, white sharks would have to scour the ocean floor for food. Three different behaviours of white sharks were employed in this study to locate prey, or the best food source: (1) moving towards prey based on the pause in the waves created by the movement of the prey. White sharks navigate to prey by undulating their body and using their senses of smell and hearing. They also engage in a chaotic search for food in the ocean. (3) The manner in which white sharks seek out adjacent food. When a good prey opportunity presents itself, great white sharks approach it and stay near it²¹. Auniform random initialization generates the starting weight parameters within the search domain, defined as

where \({p}_{r}^{i}\) is the initial vector of the \({i}^{th}\) data in the \({r}^{th}\) dimension. \({S}_{r}\) and \({e}_{r}\) are the upper and lower bounds of the data, respectively, with \(j\) random number of data and ranges between [0,1].

The available size of a weight parameter is given by

where \(h\) is the current iteration,\(\upsilon_{h}\) are the weight parameters’ current iterations, \(m1\) and \(m2\) represent the learning factors \(H_{{tbest_{h} }}\) and,\(H_{h}\) respectively, \(H_{{tbest_{h} }}\) represents the optimal weight in the subgroup,\(H_{h}\) is the solution obtained a the \(h^{th}\) iteration and \(x1\) and \(x2\) are random numbers.

The convergence behavior for the optimized weight parameter is given by

where rand(1, a) is a random number in the range [0,1]. Then,

where \(m_{\max }\) denotes the maximum weight in the neural network, \(m_{\min }\) indicates the minimum of weight in the neural network, and \(R\) is the total number of iterations. The weight parameter in the neural network is calculated as;

where \(f_{\min }\) and \(f_{\max }\) denote the minimum and maximum possibilities, respectively.

Suppose the crossover probability and mutation probability of an individual with a maximum fitness value in the weight parameter is

Then, calculating the fitness value of a maximum heart disease diagnosis is given by \({L}_{min}\), representing the minimum probability of obtaining the minimum fitness value, \({L}_{max}\) denotes the probability of obtaining maximum fitness, \(L\) is the fitness of the weight parameter, \({K}_{avg}\) indicates the average fitness of the weight parameter and \({K}_{max}\) is the maximum fitness function.